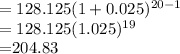Question

A local company has K2,500 to set up an annuity to be paid quarterly for 5 years. The payments of that annuity are to be increased in line with the current interest rate. The account pays interest at 10% p.a. compounded quarterly,

a) Calculate the size of each payment during the first year.

b) What is the size of the final payment (payment at the end)?​

Answer 1

Explanation:

(a).

Within 1 year, there would be 4 payments to be made.

therefore, PMT=
`(P(1+i))/(n) = (2500(1+0.025))/(4*5) =(2562.5)/(20) = $128.125`

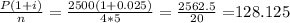
(i) 1st payment will be :PMT $128.125

(ii) 2nd payment will be :128.125*(1.025)^1= $131.33

(iii) 3rd payment will be :128.125*(1.025)^2=$134.61

(iv) 4th payment will be :128.125*(1.025)^3=$137.98

Hence the payments are: $128.125, $131.33, $134.61, and $137.98.

(b).

The size of the final payment
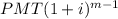`PMT(1+i)^(m-1)` where m 4 *5= 20

`=128.125(1+0.025)^(20-1) \\=128.125(1.025)^(19) \\=$204.83`