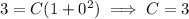Question

Solve the initial value problems.


`xy' + (x + 1)y = 0, \\ y(1) = 2`
and

`(1 + {x}^(2) )y' - 2xy = 0, \\ y(0) = 3`
​

Answer 1

Both equations are linear, so I'll use the integrating factor method.

The first ODE

`xy' + (x+1)y = 0 \implies y' + \frac{x+1}x y = 0`

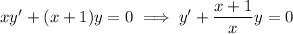
has integrating factor

`\exp\left(\displaystyle \int\frac{x+1}x \, dx\right) =\exp\left(x+\ln(x)\right) = xe^x`

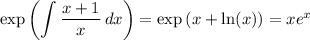
In the original equation, multiply both sides by eˣ :

`xe^x y' + (x+1) e^x y = 0`

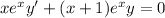
Observe that

d/dx [xeˣ] = eˣ + xeˣ = (x + 1) eˣ

so that the left side is the derivative of a product, namely

`\left(xe^xy\right)' = 0`

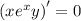
Integrate both sides with respect to x :

`\displaystyle \int \left(xe^xy\right)' \, dx = \int 0 \, dx`

`xe^xy = C`

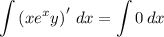
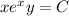
Solve for y :

`y = (C)/(xe^x)`

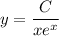
Use the given initial condition to solve for C. When x = 1, y = 2, so

`2 = (C)/(1\cdot e^1) \implies C = 2e`

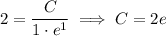
Then the particular solution is

`\boxed{y = (2e)/(xe^x) = \frac{2e^(1-x)}x}`

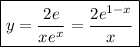
The second ODE

`(1+x^2)y' - 2xy = 0 \implies y' - (2x)/(1+x^2) y = 0`

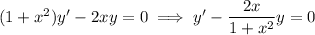
has integrating factor

`\exp\left(\displaystyle \int -(2x)/(1+x^2) \, dx\right) = \exp\left(-\ln(1+x^2)\right) = \frac1{1+x^2}`

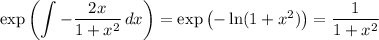
Multiply both sides of the equation by 1/(1 + x²) :

`\frac1{1+x^2} y' - (2x)/((1+x^2)^2) y = 0`

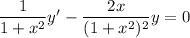
and observe that

d/dx[1/(1 + x²)] = -2x/(1 + x²)²

Then

`\left(\frac1{1+x^2}y\right)' = 0`

`\frac1{1+x^2}y = C`

`y = C(1 + x^2)`

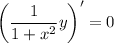
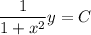
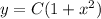
When x = 0, y = 3, so

`3 = C(1+0^2) \implies C=3`

`\implies \boxed{y = 3(1 + x^2) = 3 + 3x^2}`