Question

What is the surface area of triangular pyramid?​

Answer 1

223.5 in²

Explanation:

The surface area of a triangular pyramid comprises:

• Area of the base triangle.
• Area of 3 congruent side triangles.

Area of a triangle

`\sf A=(1)/(2)bh`

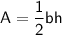
where:

• b = base
• h = height

From inspection of the diagram:

• Base triangle: b = 10 in, h = 8.7 in
• Side triangles: b = 20 in, h = 12 in

`\begin{aligned}\implies \textsf{Area of the base triangle} & = \sf (1)/(2) \cdot 10 \cdot 8.7\\& = \sf 5 \cdot 8.7\\& =\sf 43.5\:in^2\end{aligned}`

`\begin{aligned}\implies \textsf{Area of a side triangle} & = \sf (1)/(2) \cdot 10 \cdot 12\\& = \sf 5 \cdot 12\\& =\sf 60\:in^2\end{aligned}`

`\begin{aligned}\implies \textsf{S.A. of the triangular pyramid} & = \textsf{base triangle}+\textsf{3 side triangles}\\& = \sf 43.5 + 3(60)\\& = \sf 43.5 + 180\\& = \sf 223.5\:in^2\end{aligned}`

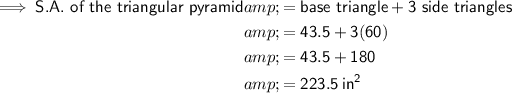
Therefore, the surface area of the given triangular pyramid is 223.5 in².