Answer:
First, plot your circle. the Center is (0, 3) and the radius is
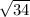
Now to find your slope move from the (0, 3) to (5, 0)
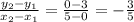
The slope of a perpendicular line is opposite and reciprocal, so the slope is
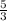
The equation of our line tangent to the circle at the point (5, 0) is
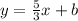
Now substitute in the point (5, 0) to solve for b

Therefore, the equation of the line tangent to the circle is
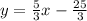
Explanation: