Question

Calculus Derivative Question

Answer 1

(a) Differentiate
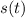`s(t)` to get the velocity.

`s(t) = \cos(t^2 - 1)`

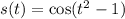
Use the chain rule.

`u = t^2 - 1 \implies (du)/(dt) = 2t`

`s(u) = \cos(u) \implies (ds)/(du) = -\sin(u)`

`\implies (ds)/(dt) = (ds)/(du) (du)/(dt) = \boxed{-2t\sin(t^2-1)}`

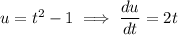
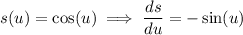
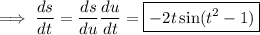
(b) Evaluate the derivative from (a) at
`t=0`.

`(ds)/(dt)\bigg|_(t=0) = -2\cdot0\cdot\sin(0^2-1) = \boxed{0}`

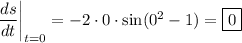
(c) The object is stationary when the derivative is zero. This happens for

`-2t \sin(t^2 - 1) = 0`

`-2t = 0 \text{ or } \sin(t^2 - 1) = 0`

`t = 0 \text{ or } t^2 - 1 = n\pi`

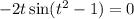
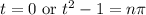
(where
`n` is any integer)

`t = 0 \text{ or } t = \pm√(n\pi + 1)`

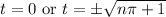
We omit the first case. In the second case, we must have
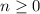`n\ge0` for the square root to be defined. Then in the given interval, we have two solutions when
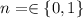`n=\in\{0,1\}`, so the times are

`t_1 = √(1) = \boxed{1}`

`t_2 = \boxed{√(\pi + 1)} \approx 2.035`

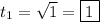
(d) A picture is worth a thousand words. See the attached plot. If you're looking for a verbal description, you can list as many features of the plot as are relevant, such as

• intercepts (solve
`s(t)=0` to find
`t`-intercepts and evaluate
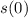`s(0)` to find the
`s`-intercept)

• intervals where
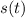`s(t)` is increasing or decreasing (first derivative test)

• intervals where
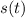`s(t)` is concave upward or concave downward (second derivative test; at the same time you can determine any local extrema of
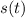`s(t)`, which you can see in the plot agrees with the critical points found in (c))