Answer

Explanation:
Greetings !
Note that:-

And also

Thus, remembering these general formula plug in values in the place of n and solve.
Therefore,
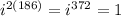
where n is even thus its 1 from the above explanation
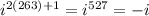
following the same procedure the values exceeds to be -i.
Hope it helps !!!