Answer:
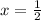 or 0.5 in decimal form
or 0.5 in decimal form
Explanation:
The expression is
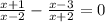
Find Least Common Multiplier (LCM) of the denominators
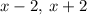
This is
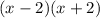 the product of the two denominators
the product of the two denominators
Multiply entire equation by this LCM:
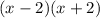
We get
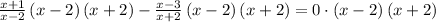
Simplify the first term
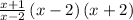
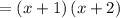
Simplify the second term
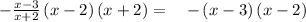
RHS is
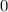
Therefore we get
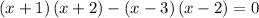
Expand the first term using the FOIL method
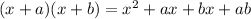
Here a = 1, b = 2. So
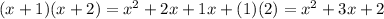
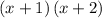
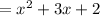
Expanding
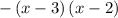 gives us
gives us
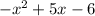
(Use the FOIL method:
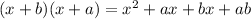 Here a = -2, b = -3. Note there is a negative sign before the entire expression)
Here a = -2, b = -3. Note there is a negative sign before the entire expression)
So the original expression is
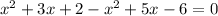
Collecting like terms
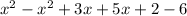
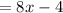 =
=
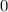
Add 4 to both sides
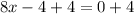
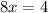
Divide both sides by 8:
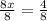
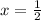 or
or
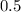 in decimal
in decimal