Consider the differential equation xy'+ y = x^2 . Without solving the equation, check which of the following are solutions: y(x) = sin(x). y(x) = (x^2)/3. y(x) = √x. y(x) =…

Question

asked Jul 8, 2023 146k views

2 Answers

Ianckc · Answer 1 · 2023-07-13T19:08:35+0000

y = √x is not a solution because y = √x has derivative also involving √x, and rational powers won't get resolved in the ODE. That is,

$y = \sqrt x \implies y' = \frac1{2\sqrt x} \implies xy'+y = \frac x{2\sqrt x}+\sqrt x = \frac32\sqrt x \\eq x^2$

Similarly, y = 5/x is not a solution because its derivative is a rational function that also doesn't get resolved.

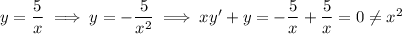
$y=\frac5x \implies y=-\frac5{x^2} \implies xy'+y = -\frac5x+\frac5x=0\\eq x^2$

In the same vein, y = sin(x) has derivative y' = cos(x), and these trigonometric expression won't get resolved in this case.

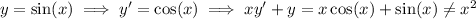
$y=\sin(x)\implies y'=\cos(x) \implies xy'+y=x\cos(x)+\sin(x) \\eq x^2$

So we focus on the remaining candidate:

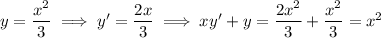
$y = \frac{x^2}3 \implies y' = \frac{2x}3 \implies xy'+y = \frac{2x^2}3+\frac{x^2}3 = x^2$

and y = x²/3 is the correct choice.