Question

(Precalc) NEED HELP 100PTS: (−2 ≤ x ≤ 2) f(x) = csc(x)

A. Find the intervals on which the graph of y = f(x) is increasing and the intervals on which the graph of y = f(x) is decreasing. Answer in interval notation.
Increasing: ___
Decreasing: ___

B. Find all relative extrema, if any, of the graph of y = f(x).
Relative min: ___
Relative max: ___

Thank youu!! <333

Answer 1

Explanation:

y=csc(x) x∈ [-2,2]

`A.\\\displaystyle\\Increasing: \ [-2,-(\pi )/(2))U((\pi )/(2),2]\\\\Decreasing:\ (-(\pi )/(2),0)U(0,(\pi )/(2) ) \\\\B.\\\\Relative\ min:\ 1\\\\Relative \ max:\ -1`

Watching the graph:

Answer 2

`\textsf{Increasing}:\left[-2,-(\pi)/(2)\right) \textsf{ and }\left((\pi)/(2),2\right]`

`\textsf{Decreasing}:\left(-(\pi)/(2), 0\right) \textsf{ and }\left(0, (\pi)/(2)\right)`

`\textsf{Relative min}: \left((\pi)/(2),1 \right)`

`\textsf{Relative max}: \left(-(\pi)/(2),-1 \right)`

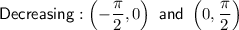
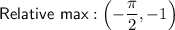
Explanation:

Part A

Given function:

`f(x)=\csc (x), \quad -2\leq x\leq 2`

`\csc(x)=(1)/(\sin(x))`

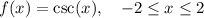
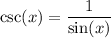
Therefore, the function f(x) is undefined when sin(x) = 0, leading to vertical asymptotes at the value of x where sin(x) = 0.

`\sin(x) = 0 \textsf{ at }x = 0\pm 2 \pi n, \pi \pm 2 \pi n`

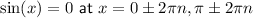
Therefore, f(x) has a vertical asymptotes at x = -2π, -π, 0, π, 2π etc.

Where the graph of the sine function increases, the graph of the cosecant function decreases.

Where the graph of the sine function decreases, the graph of the cosecant function increases.

The sine function increases on the intervals:

`\left(-(\pi)/(2)\pm 2 \pi n, (\pi)/(2)\pm 2 \pi n\right)`

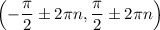
and decreases on the intervals:

`\left((\pi)/(2)\pm 2 \pi n, (3\pi)/(2)\pm 2 \pi n\right)`

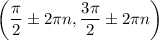
Therefore, for the interval -2 ≤ x ≤ 2, the cosecant function f(x):

Increases on the intervals:

`\left[-2,-(\pi)/(2)\right) \textsf{ and }\left((\pi)/(2),2\right]`

Decreases on the intervals:

`\left(-(\pi)/(2), 0\right) \textsf{ and }\left(0, (\pi)/(2)\right)`

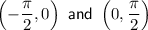
Part B

The relative minimums of the graph of the sine function are the relative maximums of the graph of the cosecant function.

The relative maximums of the graph of the sine function are the relative minimums of the graph of the cosecant function.

The sine function has a range of -1 ≤ sin(x) ≤ 1.

Therefore, its minimum points are when sin(x) = -1 and its maximum points are when sin(x) = 1.

`\sin(x)=-1 \implies x=(3\pi)/(2)\pm 2 \pi n \implies \textsf{Minimum points}: \left((3\pi)/(2)\pm 2 \pi n ,-1 \right)`

`\sin(x)=1 \implies x=(\pi)/(2)\pm 2 \pi n \implies \textsf{Maximum points}: \left((\pi)/(2)\pm 2 \pi n,1 \right)`

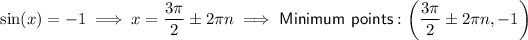
Therefore, the minimum and maximum points of the cosecant function in the given interval -2 ≤ x ≤ 2 are:

`\textsf{Relative min}: \left((\pi)/(2),1 \right)`

`\textsf{Relative max}: \left(-(\pi)/(2),-1 \right)`

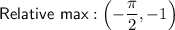
Note in the attached graph:

• The given interval -2 ≤ x ≤ 2 is shown shaded in green.
• Vertical asymptotes are shown as red dashed lines.
• Function f(x) is the black curve.
• The sine function is the blue dashed curve.
• Relative min/max shown as black points.