Question

Find the Inverse Function : Algebra 2

y = 2x² + 1​

Answer 1

`\displaystyle\\Answer:\ y=\sqrt{(x-1)/(2) } \ \ \ \ (x\geq 1,\ \ \ \ y\geq 0)`

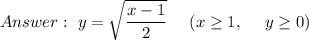
Explanation:

`y=2x^2+1\\`

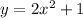
We change the argument and the value:

`\displaystyle\\x=2y^2+1\\\\x-1=2y^2+1-1\\\\x-1=2y^2\\`

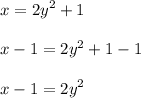
Divide both parts of the equation by 2:

`\displaystyle\\(x-1)/(2)=y^2\\\\ \sqrt{(x-1)/(2) }=y \ -\ the\ desired\ inverse\ function\\\\`

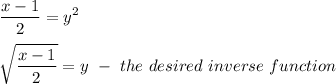
The restrictions are imposed on the inverse function by on x:

`x-1\geq 0\\x\geq 1`

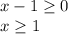
The restrictions are imposed on the inverse function by on y:

`y\geq 0`

Then the original function is defined on the sets:

`x\geq 1,\ \ \ \ y\geq 0`

The initial function, a parabola, is constrained because of the inverse function; only in this case the functions are reciprocal.