Question

A preparation of drug granules weighing 2 g with a total surface area of (0.35 × 104 cm2) is allowed to dissolve in 250 mL water at 25 °C. After the first minute, 0.25 g has passed into solution. If the solubility (Cs) of the drug is 20 mg/mL at 25 °C, calculate the dissolution rate

a.

4.2 mg/min

b.

4.2 mg/sec

c.

4.2 mg/mL

d.

250 mg/sec

​

Answer 1

Step-by-step explanation:

The Noyes-Whitney equation is often used to predict the rate at which solid substances, such as drug tablets and granules, in a solvent. Hence, according to the Noyes-Whitney equation, the dissolution rate of a drug tablet or granule can be evaluated in accordance with the following expression

`\displaystyle(dm)/(dt) \ = \ A \ \displaystyle(D)/(h)(C_(s) - C_(b))`,

where
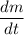`\displaystyle(dm)/(dt)` is the rate of dissolution,
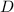`D` is the dissociation coefficient,
`h` is the thickness of the diffusion layer,
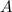`A` is the surface area of the solute particle,
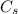`C_(s)` is the particle surface (saturation) concentration and
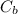`C_(b)` is the concentration in the bulk solvent.

In the case of the question, we need to find the dissolution rate of the drug granules which corresponds to the first-order differential term,
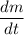`\displaystyle(dm)/(dt)`. Looking closely at this term, it implies that the dissolution rate is defined by the change of the solute mass,
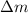`\Delta m`, with respect to the change in time,
`\Delta t`.

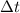In accordance with the given description from the question, we know that 0.25g of the 2g drug granules had dissolved into the solution over a period of 1 minute. Using dimensional analysis, we can simply calculate the dissolution rate as

`\displaystyle(dm)/(dt) \ = \ \displaystyle(\Delta m)/(\Delta t) \\ \\ \-\hspace{0.7cm} = \ \displaystyle\frac{(0.25 * 10^3) \ \text{mg}}{60 \ \text{sec}} \\ \\ \-\hspace{0.7cm} = \ \displaystyle\frac{250 \ \text{mg}}{60 \ \text{sec}} \\ \\ \-\hspace{0.7cm} = \ 4.2 \ \text{mg sec}^(-1) \ \ \ \ \ (1 \ \text{d.p.})`