Question

(1-tan4 A) cos4 A = 1-2 sin² A​

Answer 1

Explanation:

You want to demonstrate the identity ...

(1-tan⁴(A))·cos⁴(A) = 1 -2·sin²(A)

Working with the left side, we have ...

`(1-\tan^4(A))\cos^4(A)=1-2\sin^2(A)\\\\(1-(\sin^4(A))/(\cos^4(A)))\cos^4(A)=1-2\sin^2(A)\qquad\text{use tangent identity}\\\\\cos^4(A)-\sin^4(A)=1-2\sin^2(A)\qquad\text{multiply it out}\\\\(\cos^2(A) +\sin^2(A))(\cos^2(A)-\sin^2(A))=1-2\sin^2(A)\qquad\text{factor}\\\\1((1-\sin^2(A))-\sin^2(A)) = 1-2\sin^2(A)\qquad\text{use $\cos^2$ identity}\\\\1-2\sin^2(A)=1-2\sin^2(A)\qquad\text{Q.E.D.}`

__

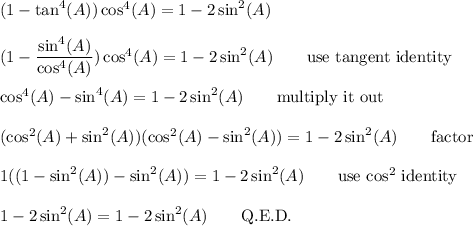
Additional comment

The referenced identities are ...

tan = sin/cos

cos² = 1 -sin²

and the factorization of the difference of squares:

a² -b² = (a +b)(a -b).