Question

The function f(x) = x² + 4 is defined on the domain [-8, 8]. Which of the following is the correct associated range?

O [4, 68]
O [0, 4]
O [-60, 4]
O (-∞, 4]
O [-60, 68]
0 (-∞, ∞)​

Answer 1

Answer: [-60, 4]

========================================================

Step-by-step explanation:

The parabola has its lowest point when either x = -8 or x = 8

Plug either value into the function

f(x) = -x^2 + 4

f(-8) = -(-8)^2 + 4

f(-8) = -60

You should find that f(8) = -60 as well

This is the lowest output possible. Confirmation of such can be done using a graph. Look for the lowest point and only focus on the interval
`-8 \le \text{x} \le 8`

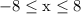
The highest point is at the vertex (0, 4), so the largest output is y = 4

------------

We have the lowest output y = -60 and the highest output y = 4

The possible set of outputs is the interval
`-60 \le \text{y} \le 4` which turns into the interval notation [-60, 4]

Check out the graph below.