Answer:
y = -3
Explanation:
You want the solution to the absolute value equation | y-4 | = | y+10 |.
Absolute value
The absolute value function ...
f(x) = | x |
is piece-wise defined as ...
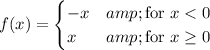
That is, the function is defined differently for argument values less than 0.
Given relation
The above observation regarding the absolute value function means the nature of the given equation changes where the absolute value arguments are zero. Those values are ...
y -4 = 0 ⇒ y = 4
y +10 = 0 ⇒ y = -10
In other words, the points y = -10 and y = 4 divide the domain of the equation into three parts. The behavior will be different in each of those parts.
To solve the equation, we must examine each region of the domain for possible solutions.
y < -10
When y < -10, both of the absolute value functions change the sign of their argument. Then the equation is ...
-(y -4) = -(y +10)
Adding y to both sides of this equation gives ...
4 = -10 . . . . . false
This means there is no solution to the equation in the region y < -10.
-10 ≤ y < 4
When -10 ≤ y < 4, the absolute value function |y -4| changes the sign of its argument, but the other function does not. In this region, the equation becomes ...
-(y -4) = (y +10)
-6 = 2y . . . . . . . . . add y-10 to both sides
-3 = y . . . . . . . . divide by 2. This value is in the region -10 ≤ y < 4.
The solution to the equation is y = -3.
4 ≤ y
When 4 ≤ y, neither absolute value function changes the sign of its argument. In this region the equation becomes ...
y -4 = y +10
Subtracting y from both sides of this equation gives ...
-4 = 10 . . . . . false
This means there is no solution to the equation in the region 4 ≤ y.
__
Additional comment
The first attached graph shows the given equation rewritten as two functions. The solution is where those functions have equal values: the point(s) where the graphs intersect.
We often find it more convenient to rewrite equations like this to the form f(x) = 0. Here, that might mean we define ...
f(x) = |y -4| -|y +10|
Then the solution is found on the graph at the x-intercepts. The graph in the second attachment shows this solution, and clearly shows the changes in behavior at x = -10 and x = 4.