Answer:
There are no values of x that make this equation true.
Explanation:
We know h(x)=
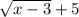
So lets substitute h(x) for 3
3=
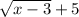
We are going to then subtract 5 from each side leaving us with
-2=
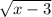
We then need to get rid of the square root, so we will square both sides. which gives us
4=x-3
We then need to subtract 3 from both sides which leaves us with
x=1
However, when you substitute 1 for x into the original equation, you get
h(x)=
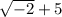
Which is not equal to 3
Therefore, there are no values of x that make this equation true.