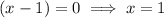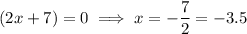Answer:
Draw a line at y = -5.
x ≈ -3.5
x ≈ 1
Explanation:
Given equation:
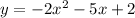
This is the equation of the graphed parabola.
To solve the equation
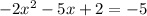 draw a line at y = -5 and find the points of intersection of the two graphed equations.
draw a line at y = -5 and find the points of intersection of the two graphed equations.
From inspection of the graph, the x-values of the points of intersection are:
Solving algebraically
Add 5 to both sides of the equation:
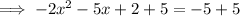
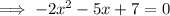
Factor out -1 from the left side:
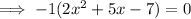
Divide both sides by -1:
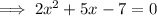
Find two numbers that multiply to -14 and sum to 5: 7 and -2
Rewrite b as the sum of these two numbers:
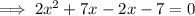
Factor the first two terms and the last two terms separately:
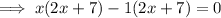
Factor out the common term (2x + 7):
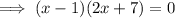
Apply the zero-product property: