Question

10. The average age of 4 boys is 14 years, when one boy leaves the group, the average age of the remaining boys becomes 15 years. How old is the 4th boy?​

Answer 1

Answer: the 4th boy is 11

Explanation:

Let's denote the age of the boys as: x₁, x₂, x₃, x₄.

Then,

`\displaystyle\\(x_1+x_2+x_3)/(3)=15`

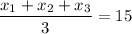
Multiply both parts of the equation by denoting by 3:

x₁+x₂+x₃=15(3)

x₁+x₂+x₃=45

Hence,

`\displaystyle\\(x_1+x_2+x_3+x_4)/(4) =14\\\\((x_1+x_2+x_3)+x_4)/(4) =14\\\\(45+x_4)/(4)=14`

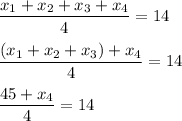
Multiply both parts of the equation by denoting by 4:

45+x₄=14(4)

45+x₄=56

45+x₄-45=56-45

x₄=11