Question

Expand and simplify root5(root10+root2)

Answer 1

25(100+4)
25(104)
= 1000

Answer 2

1. The expanded and simplified form of
`\( √(5)(√(10)+√(2)) \) is \( √(50) + √(10) \).`

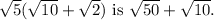
Step-by-step explanation:

To expand and simplify
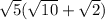`\( √(5)(√(10)+√(2)) \)`, we use the distributive property. We distribute
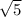`\( √(5) \)`to both terms inside the parentheses.

The expression becomes
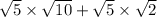`\( √(5) * √(10) + √(5) * √(2) \)`. To simplify this, we multiply the terms inside each square root:
`\( √(50) + √(10) \)`.

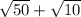Finally, we express
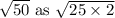`\( √(50) \) as \( √(25 * 2) \)`and simplify further to
`\( 5√(2) \)`. The simplified and expanded form is
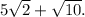`\( 5√(2) + √(10) \).` This is the final answer after expanding and simplifying the given expression.

In summary, by distributing
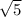`\( √(5) \)`to each term inside the parentheses and simplifying the square roots, we obtain
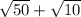`\( √(50) + √(10) \)`, which can be further simplified to
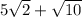`\( 5√(2) + √(10) \)`.