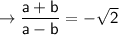Answer:
Explanation:
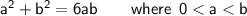
Basic formula:
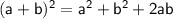
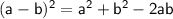
solve for a + b
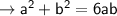
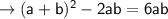
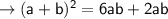
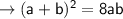
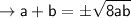
solve for a - b
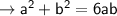
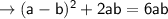
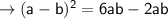
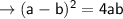
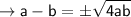
Now solve for (a + b)/(a - b)
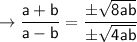
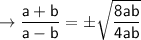
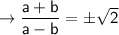
As, the value of b is greater than the value of a and both the values a and b are greater than 0. It turns the value of expression negative as the denominator will be always evaluated to negative integer and the numerator value always > 0. So, the answer will be negative, -√2.