Let a be the first term in the arithmetic sequence. Since it's arithmetic, consecutive terms in the sequence differ by a constant d, so the sequence is
a, a + d, a + 2d, a + 3d, …
with the n-th term, a + (n - 1)d.
The sum of the first n terms of this sequence is given:

We can simplify the left side as
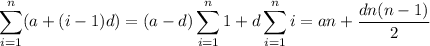
so that
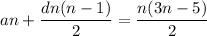
or
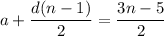
Let b be the first term in the geometric sequence. Consecutive terms in this sequence are scaled by a fixed factor r, so the sequence is
b, br, br ², br ³, …
with n-th term br ⁿ⁻¹.
The second arithmetic term is equal to the second geometric term, and the fourth arithmetic term is equal to the third geometric term, so
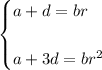
and it follows that
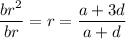
From the earlier result, we then have
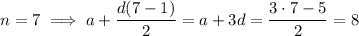
and
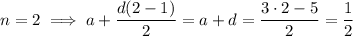
so that
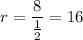
and since the second arithmetic and geometric terms are both 1/2, this means that
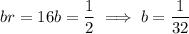
The sum of the first 11 terms of the geometric sequence is
S = b + br + br ² + … + br ¹⁰
Multiply both sides by r :
rS = br + br ² + br ³ + … + br ¹¹
Subtract this from S, then solve for S :
S - rS = b - br ¹¹
(1 - r ) S = b (1 - r ¹¹)
S = b (1 - r ¹¹) / (1 - r )
Plug in b = 1/32 and r = 1/2 to get the sum :
