Question

The publisher of a newsletter uses the following models to estimate monthly sales revenue (R) and the monthly cost of production (C), in terms of the number of people who subscribe to the news paper (X).

R(X) = 35x - 0.25x^2
C(X) = 300 + 15x

C and R are both given in thousands of euros. The value of x for which revenue is equal to cost are called "break-even" points.

Questions:
a. Write down an equation, in terms of x, to find the break-even points.
b. Solve your equation in a by completing the square.
c. Write down the number of subscribers at which newspaper sales break-even
Profit is equal to revenue minus cost.
d. Find the number of subscribers that yields maximum profit.
e. Find the maximum profit.

Answer 1

`\textsf{a)} \quad 35x-0.25x^2=300+15x`

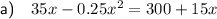
b) x = 20, x = 60

c) 20 and 60

d) 40

e) 100,000 euros

Explanation:

Given functions:

`\begin{cases}R(x)=35x-0.25x^2 \\C(x)=300+15x \end{cases}`

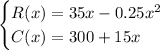
where:

• R(x) = monthly sales revenue (in thousands of euros).
• C(x) = cost of production (in thousands of euros).
• x = number of people who subscribe to the newspaper.

Part (a)

As the "break-even points" are the values of x for which the revenue is equal to the cost, an equation to find the break-even points in terms of x is:

`35x-0.25x^2=300+15x`

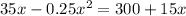
Part (b)

Rewrite the equation found in part (a) so that only the constant is on the right side:

`\implies -0.25x^2+20x=300`

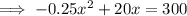
Multiply everything by -4 so that the coefficient of x² is 1:

`\implies x^2-80x=-1200`

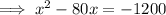
Add the square of half the coefficient of x to both sides of the equation. This forms a perfect square trinomial on the left side:

`\implies x^2-80x+\left((-80)/(2)\right)^2=-1200+\left((-80)/(2)\right)^2`

`\implies x^2-80x+1600=-1200+1600`

`\implies x^2-80x+1600=400`

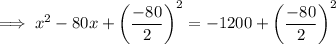
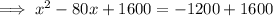
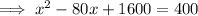
Factor the perfect square trinomial on the left side:

`\implies (x-40)^2=400`

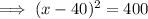
Square root both sides:

`\implies √( (x-40)^2)=√(400)`

`\implies x-40=\pm20`

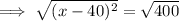
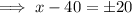
Add 40 to both sides:

`\implies x=40\pm20`

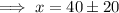
Therefore:

`\implies x=20, 60`

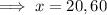
Part (c)

The number of subscribers at which the newspaper sales break-even is 20 and 60.

Part (d)

`\begin{aligned}\sf Profit & = \sf Revenue - Cost\\\implies P(x) & = R(x)-C(x)\\& = (35x-0.25x^2)-(300+15x)\\& = 35x-0.25x^2-300-15x\\& = -0.25x^2+20x-300\end{aligned}`

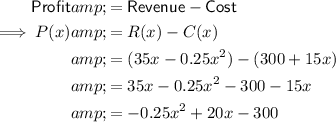
The number of subscribers that yields maximum profit will be the x-value of the vertex. The x-value of the vertex of the quadratic function P(x) is:

`\implies x \sf =(-b)/(2a)=(-20)/(2(-0.25))=(-20)/(-0.5)=40`

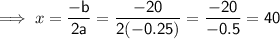
Therefore, 40 subscribers yield maximum profit.

Part (e)

To find the maximum profit, substitute the found value of x from part (d) into the function for profit P(x):

`\begin{aligned}\implies P(40) & = -0.25(40)^2+20(40)-300\\& = -0.25(1600)+20(40)-300\\& = -400+800-300\\& = 400-300\\& = 100\end{aligned}`

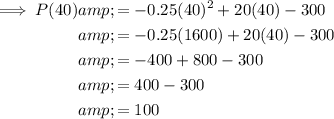
Therefore, the maximum profit is €100,000.