Question

Iam struggling with this one someone please help me:(

Answer 1

x = 26.244

Explanation:

Let the angle opposite the side of length 15 be A and the angle opposite the side with length 18 be B

if a is the side with length 18 and b is the side with length 15

then the relationship between the two know sides a and b and the included angle C is given by the law of cosines

`x^2 = a^2 + b^2 - 2ab \cos(C)`

`x^2 = 18^2 + 15^ 2 - 2\cdot18\cdot15\cdot\cos(105)`

`x^2 = 324 + 225 - 540cos(105)`

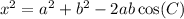
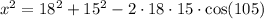
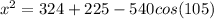
cos(105) = -0.2588

`x^2 = 324 + 225 -540(-0.2588)\\`

`324 + 225 = 549`

`(-540)(-0.2588) = - 139.75`

`x^2 = 549 - (- 139.75) = 688.75`

`x^2 = 549 + 139.75 = 688.75`

`x = \pm√(688.75) = \pm26.244`

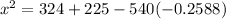
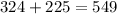
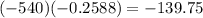
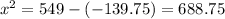
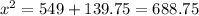
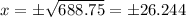
Since x cannot be negative,

x = 26.244 Answer