Answer:
(1.79, 7.58)
Explanation:
Standard form equation of a circle with center (h,k) and radius r is
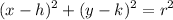
Use h = 0, k = 4 and r=4 to give
-->
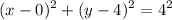
-->
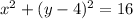
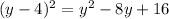
The line is
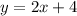
Substitute for this value of y in Equation (1)
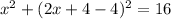
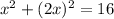
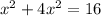
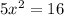
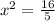
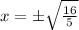
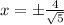
Since we are asked to find point of intersection only on the first quadrant, we ignore the negative value of x
So
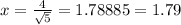 (rounded to 2 decimal places)
(rounded to 2 decimal places)
Substituting this value of x in
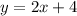
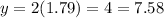
So the intersection point is at
(1.79, 7.58)
See attached graph