Answer:
Buoyant force stays the same as long as the entire object is submerged in water.
Step-by-step explanation:
Consider an object of volume
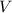 . If this object is completely submerged in a liquid of uniform density, the volume of the liquid displaced would be equal to
. If this object is completely submerged in a liquid of uniform density, the volume of the liquid displaced would be equal to
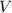 .
.
Let
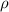 denote the density of this liquid. The mass of the liquid displaced would be
denote the density of this liquid. The mass of the liquid displaced would be
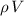 . If the gravitational field strength is
. If the gravitational field strength is
 , the weight of the liquid displaced would be
, the weight of the liquid displaced would be
 .
.
The magnitude of the buoyant force on this object would be equal to that of the weight of the water displaced,
 .
.
As long as the object is completely submerged, the volume
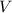 of liquid displaced does not depend on the depth of the object. Assume that
of liquid displaced does not depend on the depth of the object. Assume that
 and the density
and the density
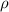 of the liquid doesn't change with depth. The weight of the liquid displaced and thus the buoyant force would be constant regardless of the depth of the object.
of the liquid doesn't change with depth. The weight of the liquid displaced and thus the buoyant force would be constant regardless of the depth of the object.
The reason is that objects submerged in water experience both upward and downward water pressure. The upward pressure is from the lower surface of the object, while the downward pressure is from the upper surface.
The buoyant force on the object depends on the difference between the two pressures. The depth of the lower surface of the object is greater than that of the upper surface. As a result, the upward pressure would exceed the downward pressure, and the object would experience an upward buoyant force.
However, note that the depth of the object does not affect the depth difference between the upper and lower surfaces of this object. If the density of the liquid is uniform, the buoyant force on the object would not depend on the depth of the object.