Key Ideas
Solving the Problem
We're given:
- Sheldon can paint 1 office in 30 minutes
- Penny can paint 1 office in 45 minutes
First, convert both the given rates to offices per hour instead of per minutes.
Sheldon:
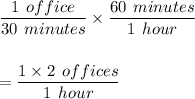
Therefore, Sheldon can paint 2 offices in 1 hour.
Penny:
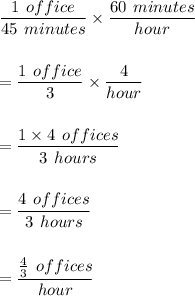
Therefore, Penny can paint
 offices in 1 hour.
offices in 1 hour.
To find their rate working together, add their individual rates:
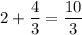
Their combined rate is
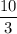 offices per hour.
offices per hour.
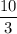 offices per hour is the same as
offices per hour is the same as
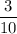 hours per office (we found the reciprocal).
hours per office (we found the reciprocal).
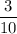 of an hour is equivalent to 18 minutes.
of an hour is equivalent to 18 minutes.
Answer
It would take them 18 minutes to paint one office working together.