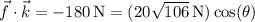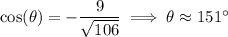Use the dot product identity
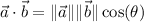
Take the dot product of
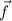 with the unit vectors
with the unit vectors
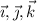 , each of whose magnitude is 1. Then compute the angles made with the
, each of whose magnitude is 1. Then compute the angles made with the
 -,
-,
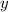 -, and
-, and
 -axis, respectively.
-axis, respectively.
Dotting with
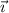 , for instance, we have
, for instance, we have
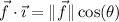
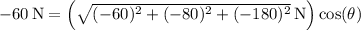
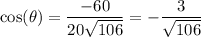
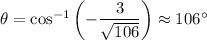
so
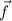 makes an angle of about 106° with the
makes an angle of about 106° with the
 -axis.
-axis.
Similarly,
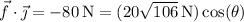
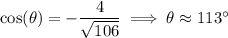
and