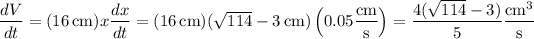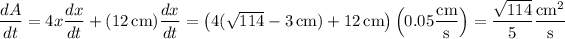Q2. By the chain rule,
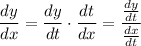
We have
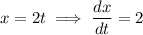

The slope of the tangent line to the curve at
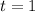 is then
is then
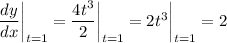
so the slope of the normal line is
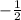 . When
. When
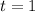 , we have
, we have
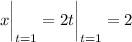

so the curve passes through (2, 2). Using the point-slope formula for a line, the equation of the normal line is
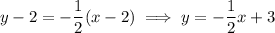
Q3. Differentiating with the product, power, and chain rules, we have
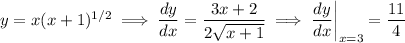
The derivative vanishes when
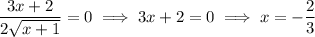
Q4. Differentiating with the product and chain rules, we have
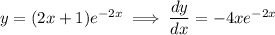
The stationary points occur where the derivative is zero.
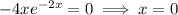
at which point we have
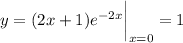
so the stationary point has coordinates (0, 1). By its "nature", I assume the question is asking what kind of local extremum this point. Compute the second derivative and evaluate it at
 .
.

The negative sign tells us this stationary point is a local maximum.
Q5. Differentiating the volume equation implicitly with respect to
 , we have
, we have

When
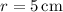 , and given it changes at a rate
, and given it changes at a rate
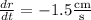 , we have
, we have
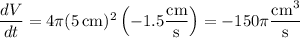
Q6. Given that
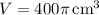 is fixed, we have
is fixed, we have
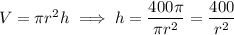
Substitute this into the area equation to make it dependent only on
 .
.
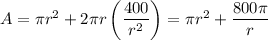
Find the critical points of
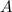 .
.
![(dA)/(dr) = 2\pi r - (800\pi)/(r^2) = 0 \implies r = (400)/(r^2) \implies r^3 = 400 \implies r = 2\sqrt[3]{50}](https://img.qammunity.org/2023/formulas/mathematics/college/sn38wxrtqbd3zjhdujtdldhkpqhl0rsmza.png)
Check the sign of the second derivative at this radius to confirm it's a local minimum (sign should be positive).
![(d^2A)/(dr^2)\bigg|_{r=2\sqrt[3]{50}} = \left(2\pi + (1600\pi)/(r^3)\right)\bigg|_{r=2\sqrt[3]{50}} = 6\pi > 0](https://img.qammunity.org/2023/formulas/mathematics/college/76a5gm9vzjfbnmgjkojz37wmxzli6vrhy9.png)
Hence the minimum surface area is
![A\bigg_{r=2\sqrt[3]{50}\,\rm cm} = \left(\pi r^2 + \frac{800\pi}r\right)\bigg|_{r=2\sqrt[3]{50}\,\rm cm} = 60\pi\sqrt[3]{20}\,\rm cm^2](https://img.qammunity.org/2023/formulas/mathematics/college/2zmg01249uu881xyvhefcdisheqk7ymo2h.png)
Q7. The volume of the box is
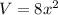
(note that the coefficient 8 is measured in cm) while its surface area is
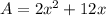
(there are two
 -by-
-by-
 faces and four 8-by-
faces and four 8-by-
 faces; again, the coefficient 12 has units of cm).
faces; again, the coefficient 12 has units of cm).
When
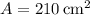 , we have
, we have
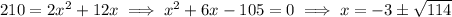
This has to be a positive length, so we have
 .
.
Given that
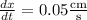 , differentiate the volume and surface area equations with respect to
, differentiate the volume and surface area equations with respect to
 .
.