Question

Solve the following using simultaneous equation
2x+5y=1
3x-2y=30

​

Answer 1

x = 8 and y = -3

Explanation:

Problem: 2x + 5y = 1; 3x − 2y = 30

1. Add -5y to both sides

⇒ 2x + 5y + −5y = 1 + −5y

⇒ 2x = -5y + 1

2. Divide both sides by 2

⇒
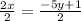
`(2x)/(2)= (-5y + 1)/(2)`

x =
`(-5)/(2)y+ (1)/(2)`

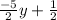
3. Substitute
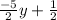`(-5)/(2)y+ (1)/(2)` for x in 3x - 2y = 30

⇒ 3x - 2y = 30

⇒
`3((-5)/(2)y+(1)/(2) )- 2y=30`

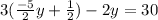
4. Simplify both sides of the equation

⇒
`-(19)/(2) +(3)/(2)=30`

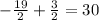
5. Add
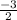`(-3)/(2)` to both sides

⇒
`(-19)/(2)y+ (3)/(2)+ (-3)/(2)=30+(-3)/(2)`

⇒
`-(19)/(2) =(57)/(2)`

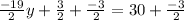
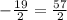
6. Divide both sides by
`(-19)/(2)`

⇒
`(-19)/(2)y\\ (-19)/(2)`=
`(57)/(2)\\ (-19)/(2)`

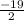
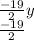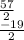
y = -3

7. Substitute -3 for y in x =
`(-5)/(2) y+(1)/(2)`

⇒
`x = (-5)/(2) y+(1)/(2)`

⇒
`x= (-5)/(2) (-3)+(1)/(2)`

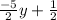
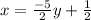
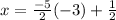
8. Simplify both sides of the equation

⇒ x = 8