Hi there,
Happy to help! So let's get into it!
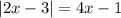
The first step to take is to solve for the Absolute Value.
Thus, we know either
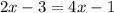 or
or
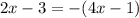
So now let's solve both possibilities:
Possibility #1

Subtract
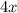 from both sides
from both sides
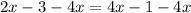
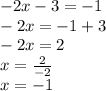
Now let's solve the second possibility
Possibility #2
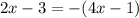
So basically here we need to simplify it. And we can start doing that by adding
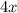 to both sides
to both sides
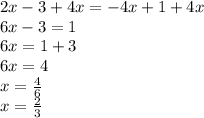
The answer is

All the best this semester!