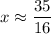Question

100 points!! ANSWER ASAP!!!!!

Answer 1

`\textsf{A.} \quad x \approx(35)/(16)`

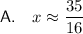
Explanation:

Given equation:

`(1)/(2)x^4-4x+1=(3)/(x-1)+2`

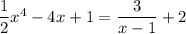
Define the left side of the equation as function f(x) and the right side as function g(x):

`f(x)=(1)/(2)x^4-4x+1`

`g(x)=(3)/(x-1)+2`

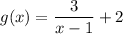
Rewrite the equation so that there is a zero on the right side:

`\implies f(x)-g(x)=0`

`\implies \left((1)/(2)x^4-4x+1\right)-\left((3)/(x-1)+2\right)=0`

`\implies (1)/(2)x^4-4x-(3)/(x-1)-1=0`

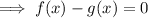
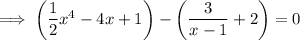
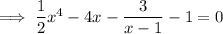
Define the bounds

From inspection of the graph, the point of intersection of the two functions is between x = 2 and x = 3. Therefore:

• Lower bound: x = 2
• Upper bound: x = 3

Substitute the x-values of the lower and upper bounds into the expression for f(x) - g(x):

`x=2 \implies (1)/(2)(2)^4-4(2)-(3)/((2)-1)-1=-4`

`x=3 \implies (1)/(2)(3)^4-4(3)-(3)/((3)-1)-1=26`

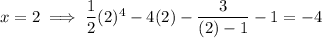
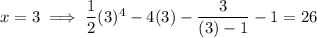
As one output is negative and the other is positive, this confirms that the solution is in the interval 2 < x < 3.

For each iteration:

• If the output has the same sign as the previous lower bound when evaluated, the average will become the new lower bound.
• If the output has the same sign as the previous upper bound when evaluated, the average is the new upper bound.

Take the average of the upper and lower bounds:

`\implies(2+3)/(2)=2.5`

First iteration

Substitute the average of the bounds into the expression for f(x) - g(x):

`x=2.5 \implies (1)/(2)(2.5)^4-4(2.5)-(3)/((2.5)-1)-1=6.53125`

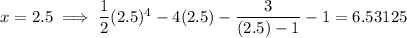
Since f(2.5) - g(2.5) is positive, and the previous upper bound is positive, x = 2.5 is the new upper bound. Therefore, the new bounds are:

• Lower bound: x = 2
• Upper bound: x = 2.5

The first approximation (after 1 iteration) for the solution to the equation is the average of the new bounds:

`\implies x=(2+2.5)/(2)=2.25`

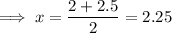
Second iteration

Substitute the average of the new bounds into the expression for f(x) - g(x):

`x=2.25 \implies (1)/(2)(2.25)^4-4(2.25)-(3)/((2.25)-1)-1=0.414453...`

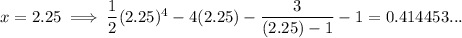
Since f(2.25) - g(2.25) is positive, and the previous upper bound is positive, x = 2.25 is the new upper bound. Therefore, the new bounds are:

• Lower bound: x = 2
• Upper bound: x = 2.25

The second approximation (after 2 iterations) for the solution to the equation is the average of the new bounds:

`\implies x=(2+2.25)/(2)=2.125`

Third iteration

Substitute the average of the new bounds into the expression for f(x) - g(x):

`x=2.125 \implies (1)/(2)(2.125)^4-4(2.125)-(3)/((2.125)-1)-1=-1.97123...`

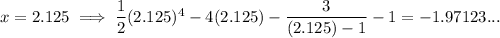
Since f(2.125) - g(2.125) is negative, and the previous lower bound is negative, x = 2.125 is the new lower bound. Therefore, the new bounds are:

• Lower bound: x = 2.125
• Upper bound: x = 2.25

The third approximation (after 3 iterations) for the solution to the equation is the average of the new bounds:

`\implies x=(2.125+2.25)/(2)=2.1875=(35)/(16)`

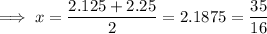
Solution

Therefore, the approximate solution to the equation using three iterations of successive approximations is:

`x \approx(35)/(16)`