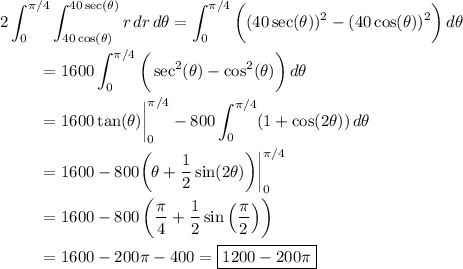First, note that
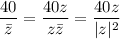
Let
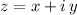 . Then we have
. Then we have
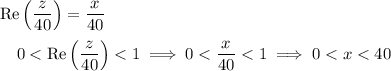
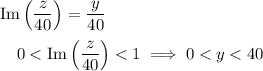

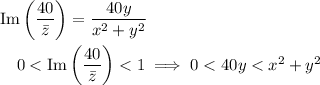
n the complex plane, the first two inequalities represent a square with vertices at 0, 40, 40 + 40i, and 40i.
The other two inequalities are regions outside disks. The boundaries are
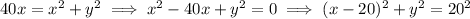
and
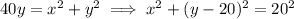
which are circles with radius 20 and centered at either (20, 0) or (0, 20).
See the attached plot of the region
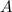 . We can use basic geometry or calculus to find its area.
. We can use basic geometry or calculus to find its area.
Geometry:
The square has area 40² = 1600. From this we subtract the area of a 20-by-20 square, whose area is 20² = 400, as well as the area of a semicircle with radius 20, whose area is π/2•20² = 200π. Then the area of
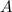 is 1600 - 400 - 200π = 1200 - 200π.
is 1600 - 400 - 200π = 1200 - 200π.
Calculus:
In polar coordinates, and taking advantage of symmetry, the area is given by the double integral
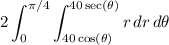
where
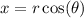 and
and
 give the polar functions
give the polar functions
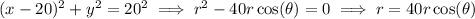
and
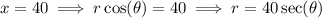
Then in the integral, we have