Answer:
Explanation:
We can solve this using the pythagorean theorem.
We know that a^2 + b^2 = c^2.
Our c value is the hypotenuse, and it does not matter what a or b is, as we will be solving for one of them.
We can set up our equation as such:
6^2 + b^2 = 20^2
From here, we can solve this algebraically.
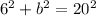
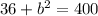
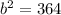
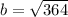
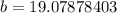
Here, b is our length for y, so y is equal to 19.07878403.