Number of hands with 0 aces, 2 non-heart queens, and at least 1 other heart:
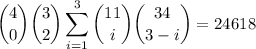
• there are 4 aces to choose from - we want none of them
• there are 3 non-heart queens to choose from - we want exactly 2 of them
• the remaining 3 cards can be 1, 2, or 3 of the 11 available hearts (13 - 1 ace - 1 queen); if
 hearts are chosen, then the other
hearts are chosen, then the other
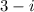 cards are non-hearts, of which there are 34 cards (52 - 13 hearts - 3 aces - 2 non-heart queens)
cards are non-hearts, of which there are 34 cards (52 - 13 hearts - 3 aces - 2 non-heart queens)
Number of hands with 0 aces, 1 heart and 1 non-heart queen, and at least 1 other heart:
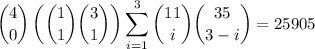
• again, there are 4 aces to choose from, which we don't want
• there is only 1 queen of hearts, and 3 other suits from which to obtain the other queen
• the remaining 3 cards can have
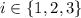 hearts from the available 11 hearts (13 - 1 queen - 1 ace), and the other
hearts from the available 11 hearts (13 - 1 queen - 1 ace), and the other
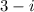 cards can be chosen from the remaining 35 cards in the deck (52 - 13 hearts - 3 aces - 1 non-heart queen)
cards can be chosen from the remaining 35 cards in the deck (52 - 13 hearts - 3 aces - 1 non-heart queen)
Then there is a total of 24618 + 25905 = 50523 such hands.