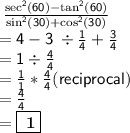Answer:
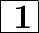
Explanation:
The key element to solve this question is to know the trignometric values of the given angles.
cosec θ, sec θ & cot θ are the reciprocals of sin θ, cos θ & tan θ respectively.
Please refer to the attachment for the trignometric values of 30°, 45° & 60° angles as they are used in the given question.

Now, let's solve this question.
First, let's write the values of the given trignometric degrees.
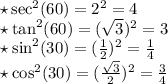
Now, let's solve the given question by substituting the above values & then simplifying by doing the necessary arithmetic operations.