Question

consider the series (-1)^(n)(x 2)^(n 1)/n! . ​(a) find the​ series' radius and interval of convergence. ​(b) for what values of x does the series conver

Answer 1

I'm assuming some plus signs are missing, and the series is

`\displaystyle \sum_(n=0)^\infty ((-1)^n (x+2)^(n+1))/(n!)`

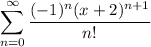
By the ratio test, the series converges for all
`x`, since

`\displaystyle \lim_(n\to\infty) \left|((-1)^(n+1) (x+2)^(n+2))/((n+1)!) \cdot (n!)/((-1)^n (x+2)^(n+1))\right| = |x+2| \lim_(n\to\infty) \frac1{n+1} = 0`

which tells us the radius of convergence is infinite, so the interval of convergence is the entire real line.

In fact, recalling that

`\displaystyle e^x = \sum_(n=0)^\infty (x^n)/(n!)`

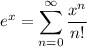
we see that

`\displaystyle \sum_(n=0)^\infty ((-1)^n (x+2)^(n+1))/(n!) = (x+2) \sum_(n=0)^\infty ((-(x+2))^n)/(n!) = (x+2) e^(-(x+2))`

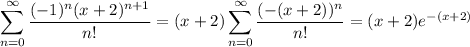
and this holds for all real
`x`.