Answer:

============================================
Work Shown:
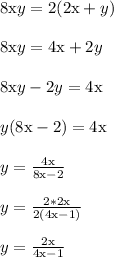
---------------
Step-by-step explanation:
The idea is to first get all the y terms to one side. I did this by subtracting 2y from both sides in the third step.
Then factor out y and divide both sides by (8x-2)
Afterward there's the optional steps of simplifying (as shown in the final two steps).