Question

If log 4 16 = log x 36, find x.

Answer 1

x = 6

Explanation:

Given the logarithmic equation:

`\displaystyle{\log_4 16 = \log_x 36}`

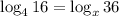
The left side can be simplified to 2 because:

`\displaystyle{\log_4 16 = x}\\\\\displaystyle{4^x = 16}`

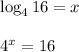
And we know that if x = 2 then it'd be true for the equation: So the left side is simplified to 2:

`\displaystyle{2 = \log_x 36}`

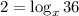
Convert logarithm to exponential where:

`\displaystyle{\log_a b = n \to a^n = b}`

Apply the property:

`\displaystyle{\log_x 36 = 2 \to x^2 = 36}\\\\\displaystyle{x^2=36}`

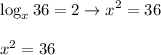
Solve the quadratic equation for x, square root both sides:

`\displaystyle{√(x^2)=√(36)`

Cancel square and add plus-minus to right side:

`\displaystyle{x=\pm √(36)}\\\\\displaystyle{x=\pm 6}`

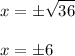
However, for logarithm function, it's defined that the base cannot be negative. Therefore, -6 is an extraneous solution while x = 6 is the only valid solution.

Therefore, x = 6.