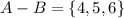Answer:
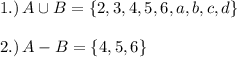
Explanation:
Given two sets which are:
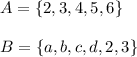
To find
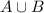 (A union B), we will simply merge both sets together - basically add all elements into one set. Therefore:
(A union B), we will simply merge both sets together - basically add all elements into one set. Therefore:
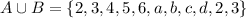
However, we do not write duplicate elements in set so we will have to take one of duplicates out. We will be able to rewrite the union set above as:
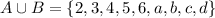
To find
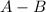 (A minus B), we will only take elements that are apart of set A.
(A minus B), we will only take elements that are apart of set A.
This means that if an element is in set A and not in set B then that element will be apart of A - B.
On the other hand, if an element is in set A but if it's also in set B then it'll be cleared out as A - B states that it'll only take in elements that are apart of set A and being apart of both sets will not count in.
Thus, 2 and 3 are not counted in since they are also apart of set B too although they both are apart of set A.
Therefore: