Answer:

Explanation:
Given the quadratic equation:
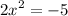
Divide both sides by 2:
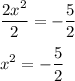
Now let's think - which real numbers multiply themselves and receive a positive value? The answer is none. It's not possible to multiply two same numbers together and receive a positive value.
Therefore, in set of real number, there are no real solutions. This equation can be solved further using complex number if you want. We will take square root both sides:

Cancel square and write plus-minus on right side of equation - same how you solve a quadratic equation in real number:

We know that a negative value cannot be inside square root as that'd result in undefined but that only applies to Real set. In complex world, we can use property of:
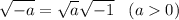
So applying the formula, we will have:
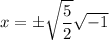
From the definition of complex number:
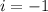
Therefore:
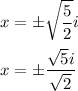
Rationalize the denominator:

Therefore, the solution in complex set is:
