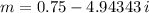Answer:
Completing the square answer

Solution set
![m = (3)/(4) + \frac{\sqrt[]{391}i}{4} = 0.75 + 4.94343 \, i](https://img.qammunity.org/2023/formulas/mathematics/college/xh24yh6111uoz9lyatchnxknawxge2xrnm.png)
![m = (3)/(4) - \frac{\sqrt[]{391}i}{4}](https://img.qammunity.org/2023/formulas/mathematics/college/mh7r82szwjbslo9e5x285iw22lub0i4zun.png) =
=
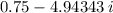
Explanation:
Assuming the question is correctly interpreted as 2m2 = 2m², here is how to proceed
We have

Divide by 2 on both sides
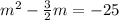
Take half of the coefficient of
 and square it
and square it
![\left[ - (3)/(2) \cdot (1)/(2) \right]^2 = (9)/(16)](https://img.qammunity.org/2023/formulas/mathematics/college/zbmt7pg4k48r0jmuk7x8abd3kwv6mofg0p.png)
Add the result to both sides
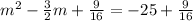
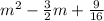 can be re-written as a perfect square
can be re-written as a perfect square
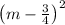
The RHS becomes
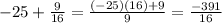
Therefore,

Take the square root of both side
![m - (3)/(4) = \pm \sqrt[]{ - (391)/(16)}](https://img.qammunity.org/2023/formulas/mathematics/college/8txnlo0exc6om2qixfaac45qjdliy14npi.png)
Simplify
![m - (3)/(4) = \pm \frac{\sqrt[]{391}i}{4}](https://img.qammunity.org/2023/formulas/mathematics/college/s1t75q3h4si2getd8ev99sb75puow3m2y8.png)
Adding
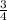 both sides
both sides
![m = (3)/(4) + \frac{\sqrt[]{391}i}{4}](https://img.qammunity.org/2023/formulas/mathematics/college/mcn63950b2prjfgbyfimcgfnq13fo4qyh0.png)
This gives the two solutions
![m= (3)/(4) + \frac{\sqrt[]{391}i}{4}](https://img.qammunity.org/2023/formulas/mathematics/college/10n1wh2i2jbq0ubkc4w3dygnvdfajtazdi.png) and
and
![m = (3)/(4) - \frac{\sqrt[]{391}i}{4}](https://img.qammunity.org/2023/formulas/mathematics/college/mh7r82szwjbslo9e5x285iw22lub0i4zun.png)
which becomes
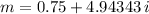 and
and