Question

Help me i do not understand this!!!!!!!!!!

Answer 1

domain is -10 <= x <= 6 which is represented in interval notation as

D= [-10, 6]

Explanation:

The domain is the set of inputs for the function where the function value is real and defined.

We can see that the function is defined only for the values between x=-10 and x = +6 (both points included)

So the domain is -10 <= x <= 6 which is represented in interval notation as

D= [-10, 6]

The square brackets on either side indicate that both -10 and 6 are included

Answer 2

`\displaystyle{-10 \leq x \leq 6}`

[-10, 6] in interval notation form

Explanation:

To determine the domain of graph, we can use the structure of:

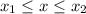`\displaystyle{x_1 \leq x \leq x_2}` if the points are closed - it means they have solid colors.

Use
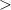`\displaystyle{ > }` or
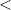`\displaystyle{ < }` if the points are opened - it means they do not have any solid colors, in other word, they are white points.

where
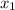`\displaystyle{x_1}` is initial point (from left side) and
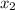`\displaystyle{x_2}` is final point (from right side). Since domain is set of all x-values, we will only be looking where the points are located at which x-value.

The initial point from left side is at x = -10 and the final point from right side is at x = 6. Follow the structure:

`\displaystyle{x_1 = -10}\\\displaystyle{x_2 = 6}`

Therefore, our domain is
`\displaystyle{-10 \leq x \leq 6}` and we use
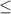`\displaystyle \leq` because those points are closed - they are solid as seen in the image.

In case if you want to use interval notation, it'd be
`\displaystyle{[-10,6]}`. We use
`\displaystyle{[}` or
`\displaystyle{]}` to represent that the points are closed while using normal bracket ( or ) will represent that the points are opened.