Question

Write the standard form of the equation of the line through the given points (0,4) and (-1,-1)

Answer 1

`5x - y = -4`

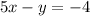
Explanation:

The standard form of a linear equation in two variables representing a line is
`ax+by+c = 0`

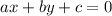
Equation of a line passing through two points
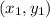`(x_1,y_1)` and
`(x_2,y_2)` is given by

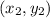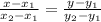`(x-x_1)/(x_2-x_1)=(y-y_1)/(y_2-y_1)` (1)

Hence, equation of line passing through
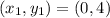`(x_1,y_1) = (0,4)` and
`(x_2, y_2) = (-1,-1)`

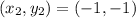
Plugging these values into equation (1) gives

`(x-0)/(-1-0)=(y-4)/(-1-4)`

`(x)/(-1)=(y-4)/(-5)`

`-x = -(y-4)/(5)`

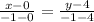
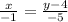
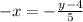
Multiplying by -5 on both sides, gives

`5x = y - 4`

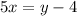
Subtracting y on both sides,

`5x - y = -4`

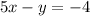
The attached graph shows the line and that it does pass through both points (0,4) and (-1,-1)