Answer: 0
=================================================
Work Shown:
f(x) = 8
f(x+h) = 8
Compute the difference quotient
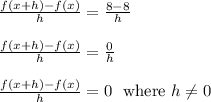
Notice that the function y = 8 is a horizontal line through 8 on the y axis. The slope of the tangent is the exact same as the linear function, so this tangent slope is also 0. This is why we end up with a difference quotient of 0.
Another thing to note is that f(x) and f(x+h) are identical simply because no x is found in the f(x) function. The output is always 8.