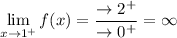Question

Pls help this is pretty urgent

Answer 1

See explanation

Explanation:

7. a. When x approaches -1, the denominator will alway be positive and close to 0. The numerator is also very close to 0. When you divide the two numbers, the answer would be 0 since the quotient is too close to 0.

b. g is f simplified.

(x^2+2x+1)/(x^2-1)=

(x+1)^2/(x+1)(x-1)=(x+1)/(x-1)

c. (1^2+2(1)+1)/(1^2-1)=

4/0.0...01 ==> ∞

When you divide a number like 4 by a very small number, the quotient gets bigger, approaching infinity.

Answer 2

(a) 0

(b) f(x) = g(x)

(c) See below.

Explanation:

Given rational function:

`f(x)=(x^2+2x+1)/(x^2-1)`

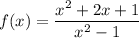
Part (a)

Factor the numerator and denominator of the given rational function:

`\begin{aligned} \implies f(x) & = (x^2+2x+1)/(x^2-1) \\\\& = ((x+1)^2)/((x+1)(x-1))\\\\& = (x+1)/(x-1)\end{aligned}`

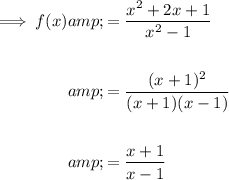
Substitute x = -1 to find the limit:

`\displaystyle \lim_(x \to -1)f(x)=(-1+1)/(-1-1)=(0)/(-2)=0`

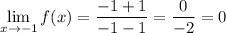
Therefore:

`\displaystyle \lim_(x \to -1)f(x)=0`

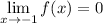
Part (b)

From part (a), we can see that the simplified function f(x) is the same as the given function g(x). Therefore, f(x) = g(x).

Part (c)

As x = 1 is approached from the right side of 1, the numerator of the function is positive and approaches 2 whilst the denominator of the function is positive and gets smaller and smaller (approaching zero). Therefore, the quotient approaches infinity.

`\displaystyle \lim_(x \to 1^+) f(x)=(\to 2^+)/(\to 0^+)=\infty`