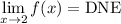Question

Pls help this is prettty urgent

Answer 1

`\textsf{(a)} \quad \displaystyle \lim_(x \to 2^+)f(x)=1`

`\textsf{(b)} \quad \displaystyle \lim_(x \to 1)f(x)`

`\sf (c) \quad c = 2`

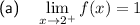
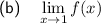
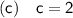
Explanation:

Part (a)

Approach x = 2 from the right side of 2:

`\displaystyle \lim_(x \to 2^+)f(x)= \lim_(x \to 2^+)(x-1)=2-1=1`

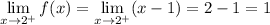
Part (b)

`\textsf{To find }\displaystyle \lim_(x \to 1)f(x):`

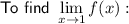
Approach x = 1 from the left side of 1:

`\displaystyle \lim_(x \to 1^-)f(x)= \lim_(x \to 1^-)(2^x)=2^1=2`

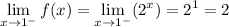
Approach x = 1 from the right side of 1:

`\displaystyle \lim_(x \to 1^+)f(x)= \lim_(x \to 1^+)(2^x)=2^1=2`

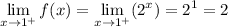
As the approach from the left and right go to the same y-value:

`\displaystyle \lim_(x \to 1^-)f(x)= \lim_(x \to 1^+)f(x)\implies \displaystyle \lim_(x \to 1)f(x)=2`

`f(2)=2-1=1`

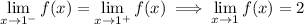
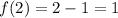
Therefore, as 2 > 1 then:

`\implies \displaystyle \lim_(x \to 1)f(x) > f(2)`

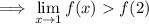
Part (c)

For a limit to exist at a point x = c, the right and left limits must be equivalent at c. From inspection of the graph, the limit for the value of c on the interval [0, 3] that does not exist is c = 2.

Approach x = 2 from the left side of 2:

`\displaystyle \lim_(x \to 2^-)f(x)= \lim_(x \to 2^-)(2^x)=2^2=4`

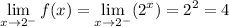
Approach x = 2 from the right side of 2:

`\displaystyle \lim_(x \to 2^+)f(x)= \lim_(x \to 2^+)(x-1)=2-1=1`

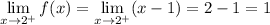
As the approach from the left and right do not go to the same y-value, the limit does not exist at c = 2:

`\displaystyle \lim_(x \to 2)f(x)= \rm DNE`