Question

Can someone please help I will mark u brilliant

Answer 1

Answer:
`(x, y) \to (x+ 8, y-6)`

=======================================================

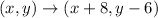
Step-by-step explanation:

Point Q has x coordinate -9

Point Q' has x coordinate -1

The horizontal movement from Q to Q' is "shift 8 units to the right". So we have x update to x+8

At the same time, we're shifting 6 units down since we go from y = 5 to y = -1. So we'll subtract 6 from the y coordinates.

The translation rule is therefore
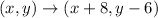`(x, y) \to (x+ 8, y-6)` to shift 8 units right and 6 units down.

----------------------

Let's apply this rule to point R to see it in action.

`(x, y) \to (x+ 8, y-6)\\\\(-6, 3) \to (-6+ 8, 3-6)\\\\(-6, 3) \to (2, -3)`

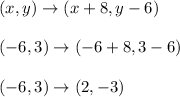
We have R(-6, 3) arrive at R ' (2, -3) which is what the graph shows. This confirms the translation rule works for point R.

I'll let you confirm this rule with points P and Q.