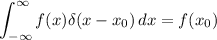Question

. use the ft analysis equation to compute the fourier transforms of: (a) e−2(t 2)u(t) (b) δ(t 3) −δ(t −3)

Answer 1

It looks like you're asked to find the Fourier transforms of (a)
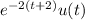`e^(-2(t+2))u(t)` and (b)
`\delta(t+3)-\delta(t-3)`.

(a) We have by definition of the Fourier transform,

`\mathcal F \left\{e^(-2(t+2))u(t)\right\} = \displaystyle \int_(-\infty)^\infty e^(-2(t+2)) u(t) e^(-i\,2\pi\xi t) \, dt \\\\ ~~~~~~~~ = \int_0^\infty e^(-2(t+2)) e^(-i\,2\pi\xi t) \, dt \\\\ ~~~~~~~~ = \frac1{e^4} \int_0^\infty e^(-(2+i\,2\pi\xi) t) \, dt`

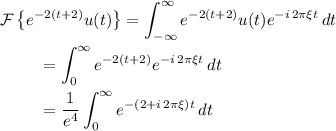
Substitute
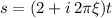`s=(2+i\,2\pi\xi)t` and
`ds = (2+i\,2\pi\xi) \, dt`.

`\mathcal F \left\{e^(-2(t+2))u(t)\right\} = \displaystyle \frac1{e^4(2+i\,2\pi\xi)} \int_0^\infty e^(-s) \, ds = \boxed{\frac1{2e^4(1+i\,\pi\xi)}}`

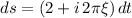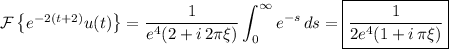
This may or may not agree with whatever solution you expect, depending on the definition you are using for the transform. For the record, I'm using the definition

`\hat f(\xi) = \displaystyle \mathcal F\left\{f(x)\right\} = \int_(-\infty)^\infty f(x) e^(-i\,2\pi\xi x) \, dx`

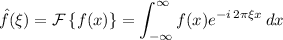
(b) The Fourier transform is

`\mathcal F\left\{\delta (t + 3) - \delta (t - 3)\right\} = \int_(-\infty)^\infty (\delta(t+3)-\delta(t-3)) e^(-i\,2\pi\xi t) \, dt \\\\ ~~~~~~~~ = e^(-i\,2\pi\xi(-3)) - e^(-i\,2\pi\xi(3)) \\\\ ~~~~~~~~ = e^(i\,6\pi\xi) - e^(-i\,6\pi\xi) \\\\ ~~~~~~~~ = 2 \sinh(i\,6\pi\xi) \\\\ ~~~~~~~~ = \boxed{2i\sin(6\pi\xi)}`

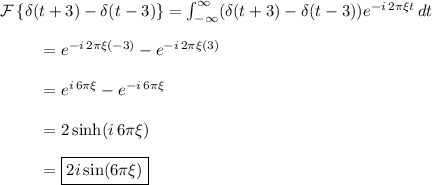
where we use the property of the delta function that

`\displaystyle \int_(-\infty)^\infty f(x) \delta(x-x_0) \, dx = f(x_0)`