Question

find the equation of the least-squares regression line ŷ and the linear correlation coefficient r for the given data. round the constants, a, b, and r, to the nearest hundredth. {(1, 2), (3, 7), (5, 10), (9, 20), (11, 22)}

Answer 1

Least-squares regression line

The following equation can represent a straight line.

`Y=\mathrm{a}+\mathrm{b} X`

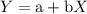
Where 'b' is the slope of the line, and "a" is the y-intercept.

For this problem,

`\begin{aligned}&b=2.0523 \\&a=0.2965\end{aligned}`

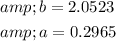
The equation of the regression line for the given problem is given below.

Y=0.30+2.05 X

The coefficients have been rounded off to the nearest hundredths.

Linear correlation coefficient

Another name for the linear correlation coefficient is Pearson's correlation coefficient. The value of the linear correlation coefficient is given below for the data in the problem.

Linear or Pearson correlation coefficient (r) = 0.9948

Calculations:

Least-squares regression line

Let's build a table with X and Y values.

X Y

1 2

3 7

5 10

9 20

11 22

Let's consider X as the independent variable and Y as the dependent variable. The following table needs to be prepared to compute the regression coefficients.

X Y X⋅Y
`X^(2)`
`Y^(2)`

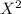
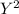
1 2 2 1 4

3 7 21 9 49

5 10 50 25 100

9 20 180 81 400

11 22 242 121 484

Sum29 61 495 237 1037

Using this table, we can do the following calculations.

`\begin{equation}\begin{aligned}&\bar{X}=(1)/(n) \sum_(i=1)^n X_i=(29)/(5)=5.8 \\&\bar{Y}=(1)/(n) \sum_(i=1)^n Y_i=(61)/(5)=12.2 \\&S S_(X X)=\sum_(i=1)^n X_i^2-(1)/(n)\left(\sum_(i=1)^n X_i\right)^2=237-29^2 / 5=68.8 \\&S S_(Y Y)=\sum_(i=1)^n Y_i^2-(1)/(n)\left(\sum_(i=1)^n Y_i\right)^2=1037-61^2 / 5=292.8 \\&S S_(X Y)=\sum_(i=1)^n X_i Y_i-(1)/(n)\left(\sum_(i=1)^n X_i\right)\left(\sum_(i=1)^n Y_i\right)=495-29 * 61 / 5=141.2\end{aligned}\end{equation}`

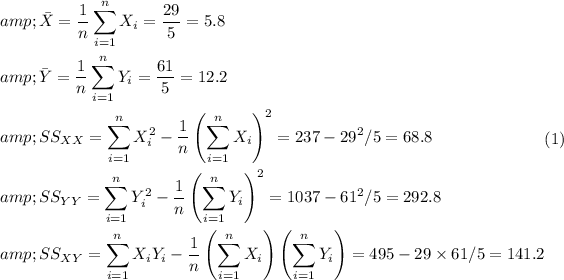
Regression coefficients like the slope "b" and the y-intercept "a" are acquired using the above calculations' values.

`\begin{equation}\begin{aligned}&b=(S S_(X Y))/(S S_(X X))=(141.2)/(68.8)=2.0523 \\&a=\bar{Y}-\bar{X} \cdot m=12.2-5.8 * 2.0523=0.2965\end{aligned}\end{equation}`

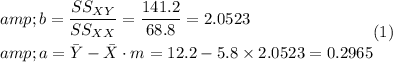
Hence, the regression line can be constructed as given below.

`\begin{equation}Y=0.30+2.05 X\end{equation}`

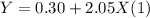
The coefficients have been rounded off to the nearest hundredths.

Linear correlation coefficient or Pearson's correlation coefficient