Question

I need help and if you can can you show how you did it?

Answer 1

Answer:
`r = \sqrt{(a)/(\pi h )}\\\\`

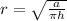
Work Shown:

`h = (a)/(\pi r^2)\\\\h r^2 = (a)/(\pi )\\\\ r^2 = (a)/(\pi h )\\\\ r = \pm \sqrt{(a)/(\pi h )}\\\\ r = \sqrt{(a)/(\pi h )}\\\\`

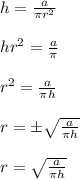
I multiplied both sides by r^2 in the second step. Then I divided both sides by h (step 3)

Apply the square root to fully isolate r. The plus minus is dropped if r is referring to the radius. A negative radius value is not possible.