Answer:
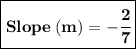
Explanation:
We are given x-coordinates and their corresponding y-coordinates.
The formula to get the slope of a line between two coordinates is:-
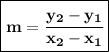
Now, that we know the formula, Let's take the third and fourth coordinates of the graph which are;
Where,
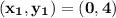
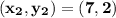
Slope: →

Subtract 2 - 4 = -2
Subtract 7 - 0 = 7
Therefore, The slope of the line that passes through the points in the table is -2/7
_________________
Hope this helps!
Have a great day!